УДК 519.233.5

Publication Text (PDF)

ПРОГНОЗИРОВАНИЕ ВАЛОВОГО РЕГИОНАЛЬНОГО ПРОДУКТА НА ОСНОВЕ КОРРЕЛЯЦИОННО-РЕГРЕССИОННОЙ МОДЕЛИ (НА МАТЕРИАЛАХ КРАСНОДАРСКОГО КРАЯ)

Мезенцева Е. В.

Филиал ФГБОУ ВО «Кубанский государственный университет» в г. Тихорецке, Тихорецк, Российская Федерация

E-mail: ekaterinamez@yandex.ru

В работе на примере Краснодарского края проведен корреляционно-регрессионный анализ для определения взаимосвязи, установления причинно-следственной зависимости между валовым региональным продуктом и отобранными факторами. Актуальность исследуемой проблематики обусловлена тем, что валовой региональный продукт является ключевым макроэкономическим индикатором социально-экономического развития региона, так как его уровень и динамика непосредственно отражают качество жизни населения, состояние социальной сферы, инвестиционный климат, конкурентоспособность территорий, развитость инфраструктуры и т. д. Соответственно прогнозирование валового регионального продукта выступает важным этапом в измерении перспектив экономической активности региона. Регрессионные модели как инструмент статистического анализа широко используются для прогнозирования социально-экономических показателей на краткосрочную или среднесрочную перспективу. Использование таких моделей позволяет не только предсказать будущее значение с высокой точностью, но и оценить влияние различных факторов на уровень ВРП.

Ключевые слова: валовой региональный продукт, прогнозирование, моделирование, корреляционно-регрессионный анализ, статистика.

Введение

Валовой региональный продукт является ключевым макроэкономическим индикатором социально-экономического развития региона, так как его уровень и динамика непосредственно отражают качество жизни населения, состояние социальной сферы, инвестиционный климат, конкурентоспособность территорий, развитость инфраструктуры и т. д. Соответственно прогнозирование валового регионального продукта выступает важным этапом в измерении перспектив экономической активности региона. Регрессионные модели как инструмент статистического анализа широко используются для прогнозирования социально-экономических показателей на краткосрочную или среднесрочную перспективу. Использование таких моделей позволяет не только предсказать будущее значение с высокой точностью, но и оценить влияние различных факторов на уровень ВРП. На основе объективных данных и прогнозов региональные органы власти принимают обоснованные экономические решения и во взаимодействии с бизнесом разрабатывают эффективные стратегии социально-экономического развития субъектов Российской Федерации.

Для написания научной статьи была использована теоретическая база работ российских и зарубежных ученых в области использования статистических методов прогнозирования [1, 2, 6], научные материалы по актуальным вопросам развития валового регионального продукта и факторов его определяющих [3], а также информационная база Федеральной службы государственной статистики (Росстат) [4].

Целью научной статьи является прогнозирование валового регионального продукта под влиянием факторов его определяющих с использованием регрессионных моделей.

В соответствии с решаемыми задачами исследования в статье использовались статистические методы анализа: динамики, табличный и графический методы представления результатов исследования, корреляционно-регрессионный анализ для определения взаимосвязи, установления причинно-следственной зависимости между ними и оценки влияния факторов на ВРП в будущем. Расчеты проведены на примере Краснодарского края.

Основной материал

Повышение валового регионального продукта свидетельствует о росте экономики, увеличении производства и расширении рынков сбыта, высоком уровне жизни и развитии региона, что способствует привлечению инвестиций, созданию новых рабочих мест и в целом росту экономики региона. Вместе с тем рост валового регионального продукта зависит от многих факторов и показателей, а существующие между ними виды связей весьма разнообразны. Корреляционно-регрессионные модели могут учитывать различные факторы, выявлять наличие и оценивать характер связей между исследуемыми переменными, предсказывать изменение результативного показателя, что имеет большое значение в решении проблемы идентификации ключевых драйверов экономического роста региона.

Для проведения прогноза на основе корреляционно-регрессионного анализа была сформирована система показателей (факторов), по нашему мнению, влияющих на уровень ВРП Краснодарского края (таблица 1). К факторам, влияющим на уровень ВРП, отнесены: численность населения, тыс. чел. (x₁), среднедушевые денежные доходы населения в месяц, руб. (x₂), инвестиции в основной капитал, млрд руб. (x₃), продукция сельского хозяйства, млрд руб. (x₄), число организаций, тыс. ед. (x₅), сальдированный финансовый результат, млрд руб. (x₆), индекс цен производителей сельскохозяйственной продукции (x₇).

Валовой региональный продукт Краснодарского края за 8 лет увеличился более чем в 2 раза и в течение исследуемого периода имеет устойчивую тенденцию роста. Также следует отметить положительную динамику у пяти отобранных факторов и напротив, за 8 лет стало меньше действующих организаций – на 26,5 % и индекс потребительских цен также снижен – более 20 %.

Построим регрессионную модель и проведем серию необходимых проверок для подтверждения ее статистической значимости.

Корреляционно-регрессионный анализ проведем с использованием табличного процессора MS Excel. Этот инструмент значительно упрощает аналитическую работу и позволяет получать результаты более оперативно.

Таблица 1. Система показателей для анализа влияния факторов на изменение валового регионального продукта Краснодарского края

Показатель	2016	2017	2018	2019	2020	2021	2022	2023	Темп роста, %
Валовой региональный продукт, млрд руб. (Y)	1934	2423	2500	2577	2667	3281	4304	4433	229,3
Численность населения, тыс. чел. (X1)	5514	5603	5648	5794	5816	5832	5819	5833	105,8
Среднедушевые денежные доходы населения в месяц, руб. (X2)	31304	33403	34372	35894	36547	42228	48684	54492	174,1
Инвестиции в основной капитал, млрд руб. (X3)	587	503	515	478	518	559	753	861	146,6
Продукция сельского хозяйства, млрд руб. (X4)	341	364	383	417	433	556	603	572	167,9
Число организаций, тыс. ед. (X5)	143	142	138	133	115	111	107	105	73,5
Сальдированный финансовый результат, млрд руб. (X6)	443	265	252	457	357	586	556	970	218,8
Индекс цен производителей сельскохозяйственной продукции (X7)	123,6	92,2	113,7	111,2	104,1	120,6	107,4	96,2	77,8

Для того чтобы выбрать фактор, наиболее тесно связанный с зависимой переменной, оценим величину влияния факторов при помощи коэффициента корреляции (рисунок 1). Отметим, что существует взаимосвязь между факторами, указывающая на проблему мультиколлинеарности. Для борьбы с этой проблемой стандартным подходом является выбор комбинации факторов, которые не взаимодействуют сильно друг с другом [2]. В данном случае такая комбинация не обнаружена, поэтому в модель включаются факторы, оказывающие наибольшее влияние. Анализ матрицы коэффициентов парной корреляции показывает, что зависимая переменная Y имеет связь средней тесноты с Х₁, Х₄ и X₅, так как коэффициенты корреляции больше 0,3, но не превышают 0,7, то есть сильной связи нет ни с одним фактором.

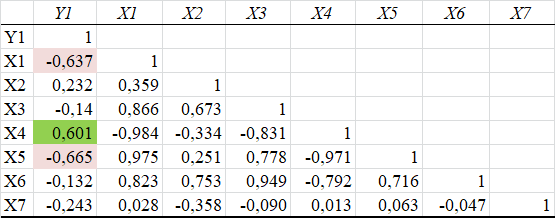
Рисунок 1. Результат корреляционного анализа

Следует отметить, что из исходной выборки были исключены факторы, имеющие слабую связь с зависимой переменной. Согласно значениям коэффициентов корреляции, представленным на рисунке 1, отобраны три фактора оказывающие умеренное влияние на валовой региональный продукт.

На основании полученных данных построена регрессионная модель:

Y = a0 + a₁ × X₁+ a₄ × X₄+ a₅ × X₅, (1)

где Х_i – факторные признаки;

а_i – неизвестные параметры уравнения (коэффициенты регрессии).

Параметры модели регрессии также вычислены с помощью надстройки МS EXCEL – Пакет анализа – Регрессия (рисунок 2).

Так как множественный R=0,948 больше 0,7, то связь между факторами Х₁, Х₄ Х₅ и Y – тесная.

Значение коэффициента детерминации R²=0,899 показывает долю вариации результативного признака под воздействием изучаемых факторов. Следовательно, 89,9 % валового регионального продукта зависят от включенных в модель факторов (численности населения, числа функционирующих организаций и объемов производства сельского хозяйства), а 10,1 % зависят от факторов, не включенных в модель.

Нормированный R–квадрат свидетельствует, что при добавлении еще одного фактора в модель, ее обхват составит 82,4 %. Таким образом, выбрано оптимальное число факторных признаков.

С использованием F–статистики проверяется, превышает ли объясненная сумма квадратов отклонений ту сумму квадратов отклонений, которая может быть случайной. Критический предел для F–статистики определяется как значение F–распределения с параметрами (уровень значимости), k (число степеней свободы числителя), n – k – 1 (число степеней свободы знаменателя) [1].

Пусть уровень значимости α = 0,05, тогда из статистической таблицы находим F_0,05;3;5 = 5,41.

Таким образом, F = 11,90 > 5,41, что означает отклонение гипотезы Н₀ при α = 0,05. Следовательно, уравнение множественной регрессии в целом является статистически значимым.

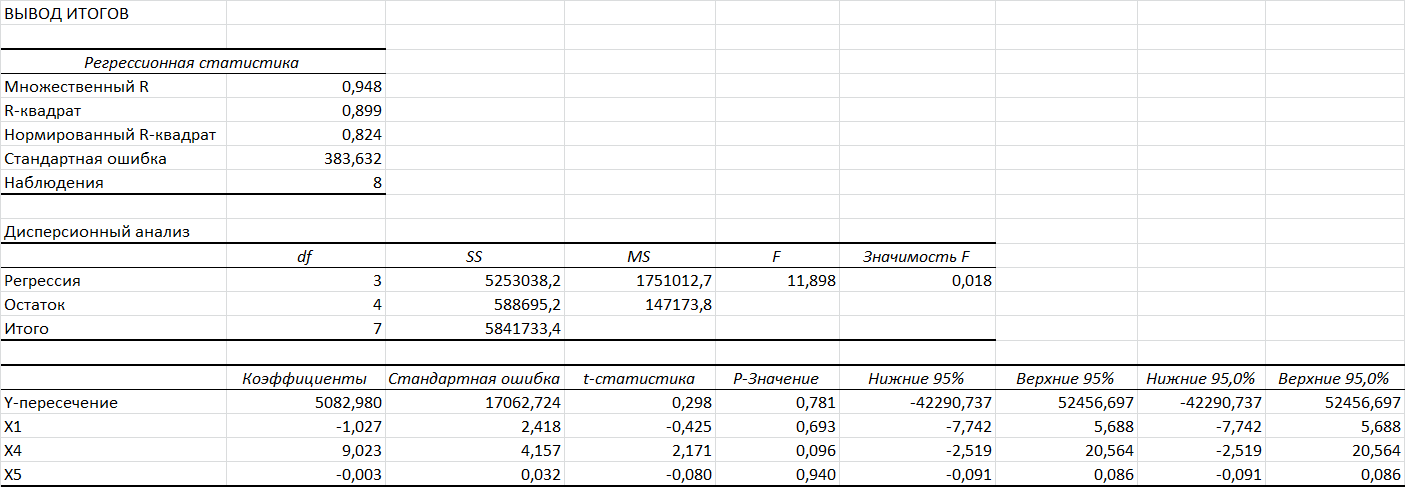
Рисунок 2. Результаты регрессионного анализа

Следовательно, уравнение регрессии зависимости валового регионального продукта от численности населения, числа функционирующих организаций и объемов производства сельского хозяйства имеет вид:

Y = 5082,980 — 1,027 × X₁+ 9,023 × X₄ — 0,003 × X₅, (2)

Параметры уравнения регрессии показывают, что при увеличении численности населения в среднем на 1 тыс. чел., валовой региональный продукт снизится в среднем на 1,027 млрд руб., при увеличении фактора Х₄ – объемов производства сельского хозяйства на 1 млрд руб. валовой региональный продукт увеличится в среднем на 9,023 млрд руб., при увеличении числа организаций в среднем на 1 тыс. ед. валовой региональный продукт снизится в среднем на 0,003 млрд руб.

Для прогнозирования величины валового регионального продукта на основе сформированной модели необходимо получить прогнозные оценки факторов X₁, Х₄, Х₅.

С использованием табличного процессора на основе инструмента величины среднего абсолютного прироста «САП» получены прогнозные оценки каждого фактора и подставлены в уравнение регрессии, которое позволило построить прогноз валового регионального продукта на 2024 и 2025 гг. Прогноз результативного показателя представлен графически на рисунке 3.

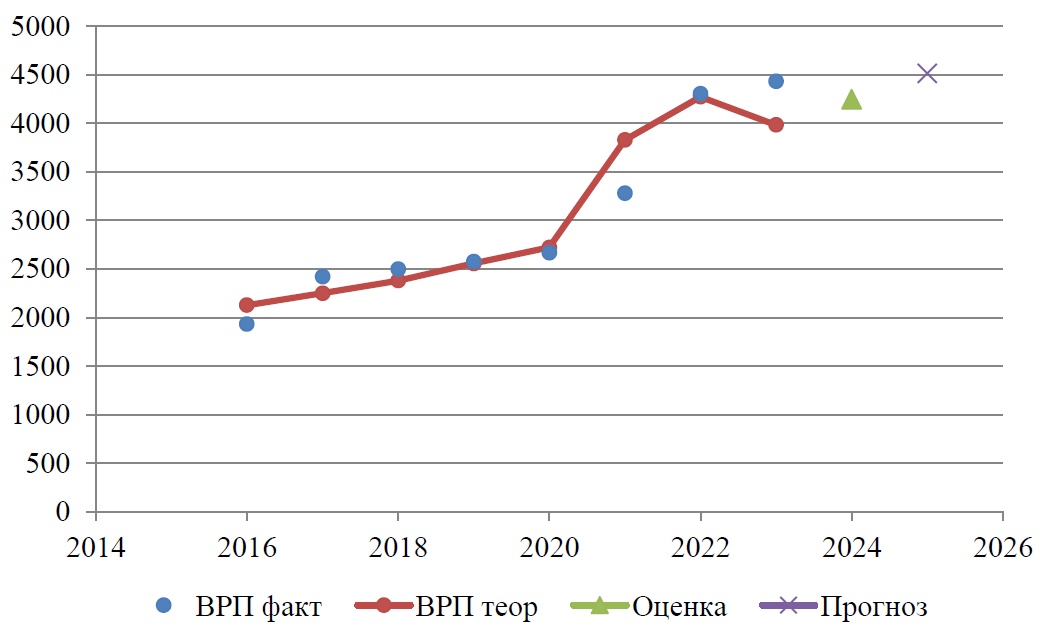
Рисунок 3. Динамика валового регионального продукта и прогноз до 2025 г.

Значение прогнозного Y является точечной оценкой валового регионального продукта в 2024 и 2025 гг. при заданных значениях независимых переменных. Она указывает, какой размер валового регионального продукта следует ожидать, если ситуация будет характеризоваться заданными значениями факторных показателей.

Выводы

Полученная нами регрессия и корреляция оказались адекватными, демонстрируя связь между валовым региональным продуктом и численностью населения, объемом производства сельскохозяйственной продукции, а также числом организаций. Нами построена модель регрессии, установлен уровень зависимости между переменными, а также представлен прогноз изменения ВРП под влиянием факторов на краткосрочную перспективу.

Применение таких моделей может быть полезным для региональных властей при разработке стратегии развития Краснодарского края. Надежные показатели позволят оценить состояние региона, распределить бюджет на основе результатов и аргументировать позицию региона на федеральном уровне.

Список литературы

1. Дегтярева Е. А. Эконометрика. Краснодар: ФГБУ «Российское энергетическое агентство» Минэнерго России Краснодарский ЦНТИ – филиал ФГБУ «РЭА» Минэнерго России, 2019. 120 с. ISBN 978-5-91221-427-1. EDN NMTWHO.
2. Садовникова Н. А., Шмойлова Р. А. Анализ временных рядов и прогнозирование. Москва: Московский финансово-промышленный университет «Синергия», 2016. 152 с. ISBN 978-5-4257-0204-3. EDN VLVFXD.
3. Карасев О. И., Кондратьева В. И., Михеева Н. Н., Шинкаренко Т. В. Повышение достоверности оценки валового регионального продукта при построении прогнозов развития региона // Вопросы статистики. 2017. № 5. С. 3–18. EDN YRGZKH.
4. Федеральная служба государственной статистики [Электронный ресурс]. URL: https://rosstat.gov.ru/folder/14036/.
5. Мезенцева Е. В. Статистика: учебно-методическое пособие. Ставрополь: Издательство Ставролит, 2016. 116 с. ISBN 978-5-903998-58-6. EDN WKWBXV.
6. Seung Hoe Choi, Hye-Young Jung, Hyoshin Kim. Ridge Fuzzy Regression Model // International Journal of Fuzzy Systems. 2019. № 21, pp 2077–2090

Статья поступила в редакцию 17.06.2024